
Ohm’s Law: Simply Explained
Introduction
Ohm’s Law is one of the most fundamental principles in electricity and electronics. It’s what helps us to describe the relationship of the current through a conductor between two points in a circuit and its direct proportionality to the electric potential difference, or voltage across those two points.
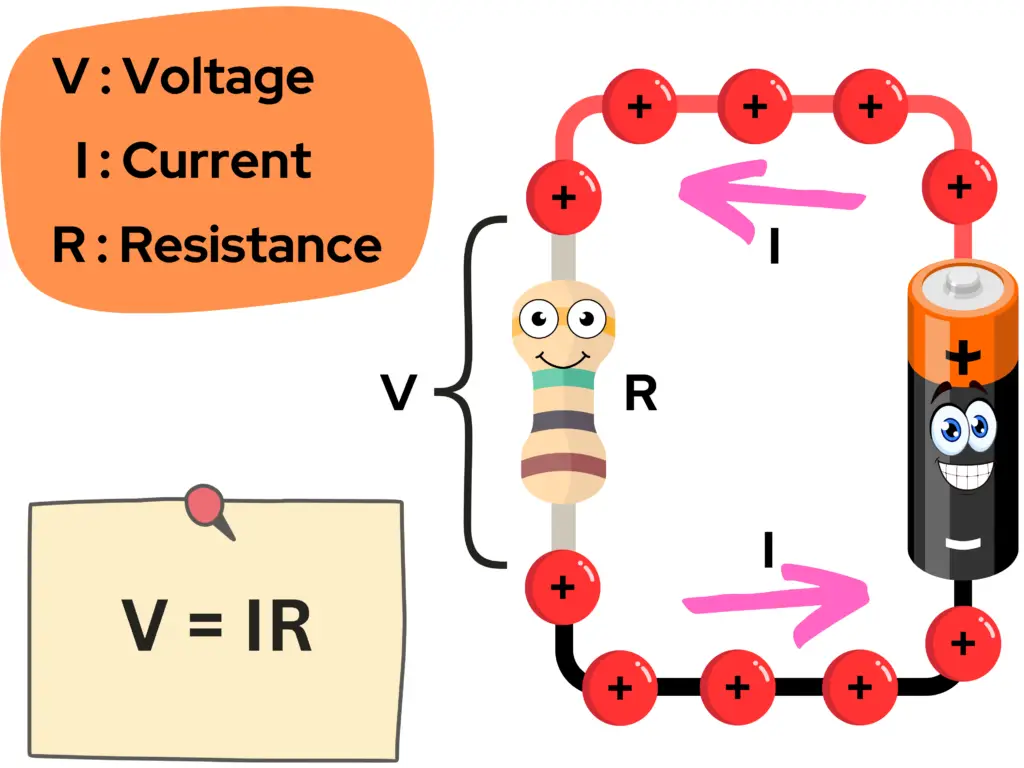
Ohm’s Law describes the relationship between three fundamental electrical quantities: voltage, current, and resistance. It states that the voltage across a conductor is equal to the current flowing through it multiplied by its resistance. In equation form, this relationship is written as V = I × R, where voltage is directly proportional to current when resistance remains constant.
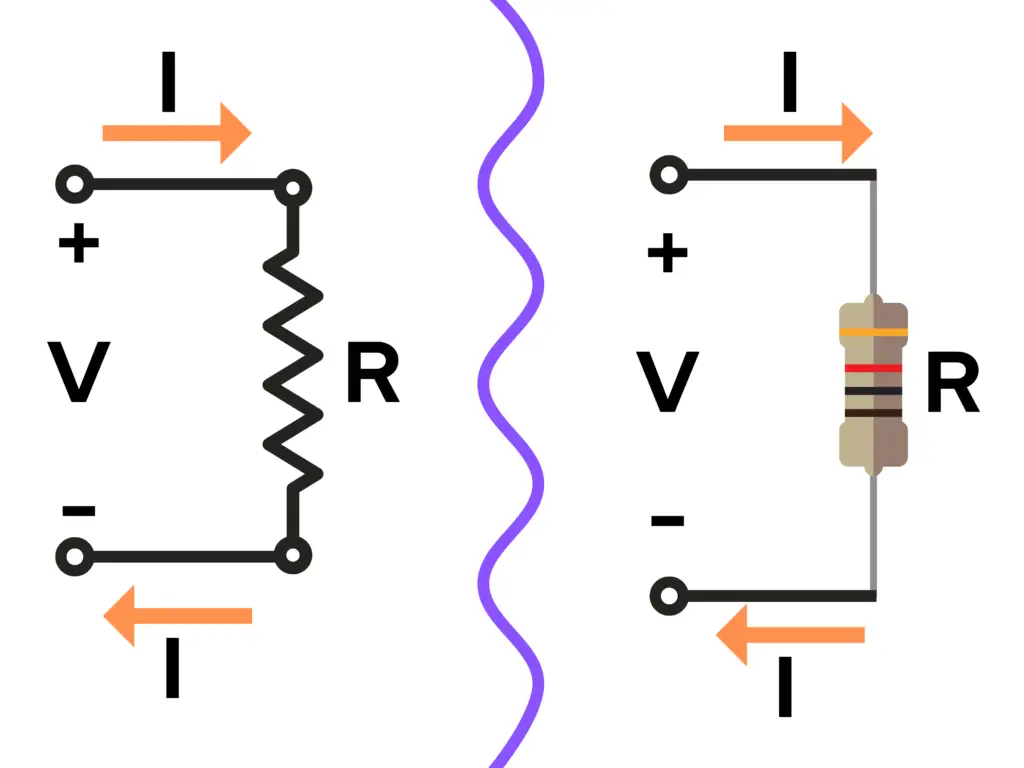
Question: What law describes the i-V characteristics for a resistor?
Answer: Ohm’s Law
\begin{equation}
V = iR
\end{equation}
Units:
\begin{equation}
R = \frac{V}{i}\quad\Longrightarrow\frac{Volts[V]}{Amps[A]} = Ohms[\Omega]
\end{equation}

Ohm’s Law: The Formula
The formula for Ohm’s Law shows that the voltage (V) is directly proportional to the product of the resistance (R) and the current (I):
\begin{equation}\label{eq:NL}
V = IR
\end{equation}
In words: “Voltage equals Current multiplied by the Resistance“
Power From the Perspective of a Resistor
\begin{equation}
P = iV
\end{equation}
\begin{equation}
P = i(iR)
\end{equation}
\begin{equation}
\boxed{P = i^{2}R}
\end{equation}

or power can be written as:
\begin{equation}
P = iV
\end{equation}
\begin{equation}
P = (\frac{V}{R})V
\end{equation}
\begin{equation}
\boxed{P = \frac{V^{2}}{R}}
\end{equation}

NOTE: Since you’re squaring the current and squaring the voltage in the latter two forms, the number for power (P) will always be positive. This is an indication that a resistor will always absorb power.
It’s recommended that you have a look at our article on active and passive elements where we discuss how some elements absorb or receive power and others supply or deliver power in a circuit.
The Water and Car Cleaning Analogy
Let’s say that it’s a beautiful summer day and your car is filthy. You think to yourself, “today is the perfect day to wash my car!” So, you grab your cleaning supplies and bucket of suds to start cleaning off the dust, dirt, mud, and bugs off your vehicle.
We’ll use the imagery of washing your car and our imagination to do an analogous comparison of electrical properties and car washing to help us understand Ohm’s Law a bit better.
Voltage
The voltage or electric potential difference measures the force that pushes electric charges through a conductor — the unit of measure being volts, represented by a V. Voltage is typically supplied by a power source, such as a battery or from a wall outlet.

Low Water Pressure
Using our water and car cleaning analogy, you can think of voltage as being the amount of water pressure your water hose has and the voltage source as compared to the supply of water coming from your local city’s water supply.
The lower the water pressure, such as a trickle out of your hose — the less pressure and power you’ll have to force the water through the nozzle to be able to spray the mud off your tires and fenders. This means more time you’re going to spend scrubbing.

Low Voltage
The lower the voltage, the less current flow and less power a circuit has — as long as the resistance stays constant.
Ohm’s Law by Example
Say you’re given the current and resistance of a circuit. The current through the circuit is 30 milliamps, and the resistor’s value is 50Ω. Find the voltage potential across the resistor.
\begin{equation}
V = IR
\end{equation}
\begin{equation}
V = (30mA)(50\Omega)
\end{equation}
\begin{equation}
V = (0.030A)(50\Omega)
\end{equation}
\begin{equation}
\boxed{V = 1.5V}
\end{equation}
High Water Pressure
The higher the water pressure, such as with using a pressure washer — the more pressure and power you’ll have to force the water through the nozzle to be able to blast the mud right off your car.

High Voltage
The higher the voltage, the more current flow and more power a circuit has — as long as the resistance stays constant.
Ohm’s Law by Example
Say you’re given the current and resistance of a circuit. The current through the circuit is 240 milliamps, and the resistor’s value is 50Ω. Find the voltage potential across the resistor.
\begin{equation}
V = IR
\end{equation}
\begin{equation}
V = (240mA)(50\Omega)
\end{equation}
\begin{equation}
V = (0.240A)(50\Omega)
\end{equation}
\begin{equation}
\boxed{V = 12V}
\end{equation}
Current
Current refers to the rate at which electric charges flow through a conductor during a given amount of time — the unit of the measure of current is the Ampere or amp, represented by an A. An amp is defined as one coulomb of charge moving past an area of a conductor in one second.
- 1 coulomb of charge is equal to the electric charge delivered by 1 ampere of current in 1 second
- 1 coulomb is defined in terms of the elementary charge e
\begin{equation}
\boxed{\text{e} \quad\approx\quad 6.241509\text{x}10^{18} \quad\text{[electrons]}}
\end{equation}
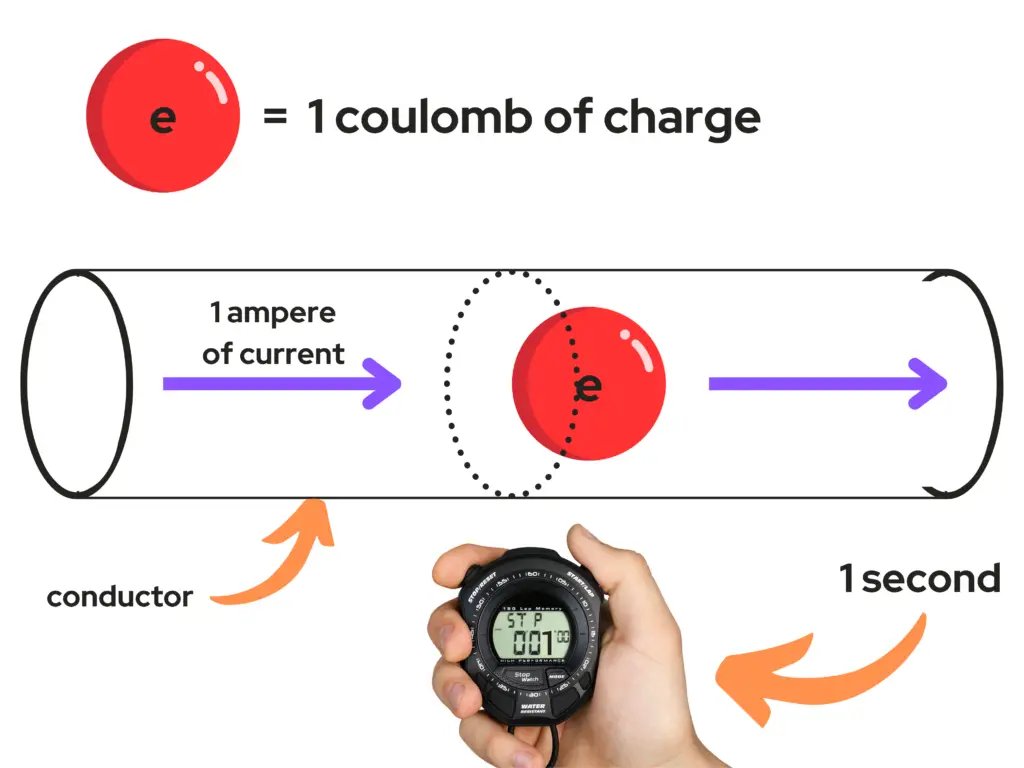
As you can see from the image above, I’ve represented a red ball as 1 coulomb of charge. I’ve used a red ball because making an image with 6,241,509,000,000,000,000 electrons would have taken me about 197,916,952,055 years at a rate of adding an electron to the image every second 😱! That’s far older than the entire universe, supposedly. Not ideal 😕.
Our 1 coulomb red ball is being delivered through the conductor by 1 ampere of current and passes through the area of the conductor represented by the dotted section. When 6.241509×1018 electrons passes through that area of the conductor in 1 second, then we have 1 coulomb of charge — as represented by the red ball in the image above.
Lower Water Pressure, Less Water Flow – Higher Water Pressure, More Water Flow
Using our water and car cleaning analogy, we can think of current as being how much water is coming out the end of the water hose at a given rate of time.
The lower the water flow, such as a trickle out of your hose — the less water flowing out the end of the water hose at a given moment in time — the less water pressure (force) you have from your water hose to wash your car.
The higher the water flow, such as when you turn the water fully on at the valve — the more water flowing out the end of the water hose at a given moment in time — the more water pressure (force) you have from your water hose to wash your car.

Lower Voltage, Less Current Flow
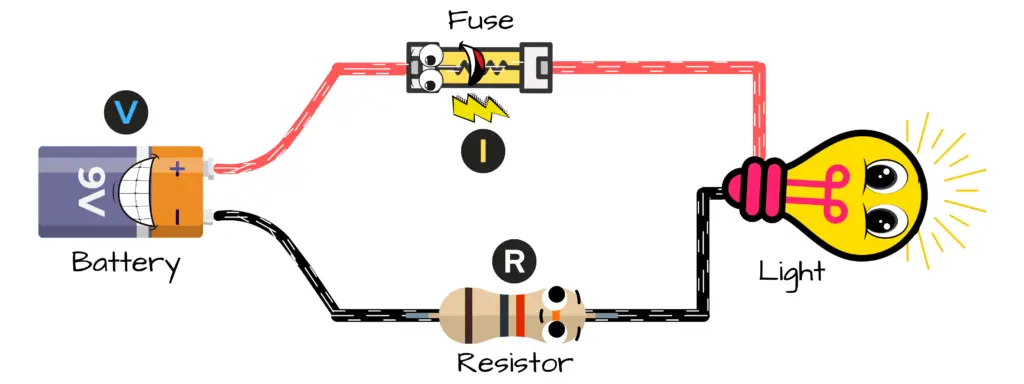

Ohm’s Law by Example
Say you’re given the voltage and resistance of a circuit. The voltage source of the circuit is 9V and the resistor value is 1000Ω. Find the value of the circuit current.
\begin{equation}
V = IR
\end{equation}
\begin{equation}
I = \frac{V}{R}
\end{equation}
\begin{equation}
I = \frac{9V}{1000\Omega}
\end{equation}
\begin{equation}
I = 0.009A
\end{equation}
\begin{equation}
\boxed{I = 9mA}
\end{equation}
Higher Voltage, More Current Flow
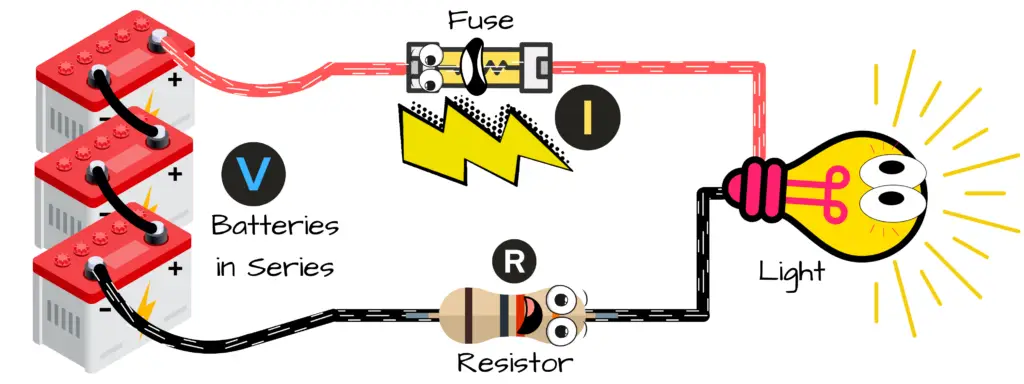

Ohm’s Law by Example
Say you’re given the voltage and resistance of a circuit. The voltage source of the circuit is 36V and the resistor value is 1000Ω. Find the value of the circuit current.
\begin{equation}
V = IR
\end{equation}
\begin{equation}
I = \frac{V}{R}
\end{equation}
\begin{equation}
I = \frac{36V}{1000\Omega}
\end{equation}
\begin{equation}
I = 0.036A
\end{equation}
\begin{equation}
\boxed{I = 36 mA}
\end{equation}
Resistance
Resistance refers to the property of material that opposes the flow of electric current. Said another way — it is the ability of a material to resist the flow of current. A resistance in a circuit is given the unit of measure in ohms (Ω).
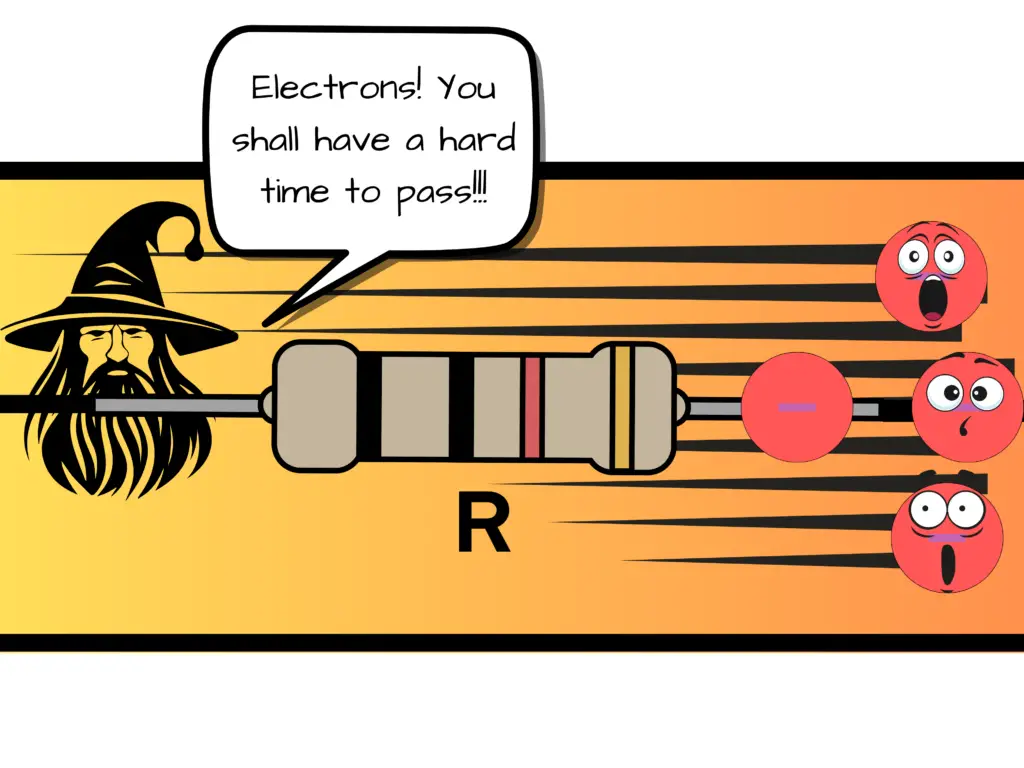
Using our water and car cleaning analogy, we can think of a resistance as being a kink in our water hose — you know when you’re using the water hose and it folds on itself not allowing water to flow through it like it should? That’s a kink, or a resistance to the flow of water.
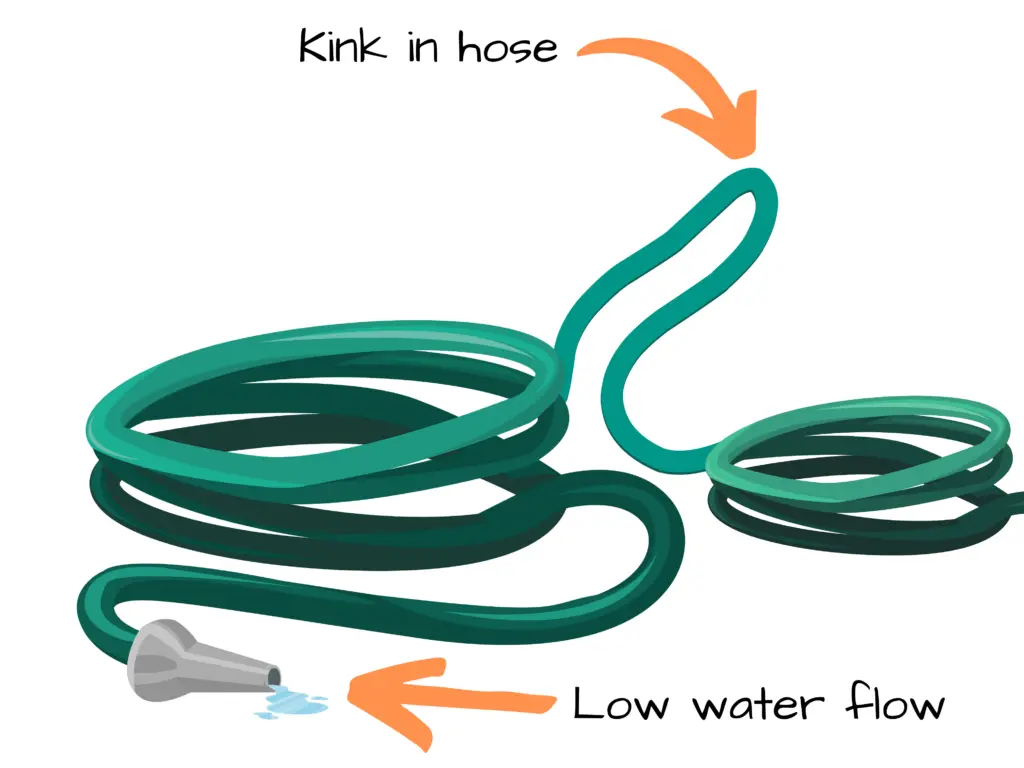
We can take the kink out of the hose so there’s no obstruction or resistance of flow for the water. Our water hose can then provide a stream of water again.
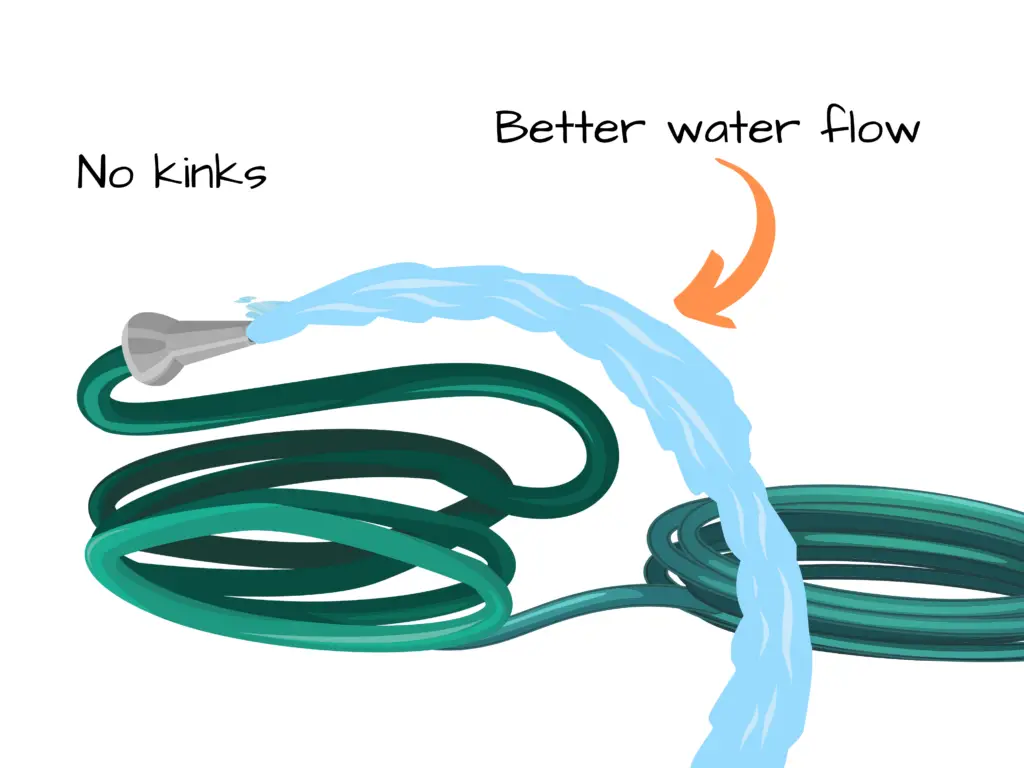
Keeping Voltage Constant – Lower Resistance, More Current Flow
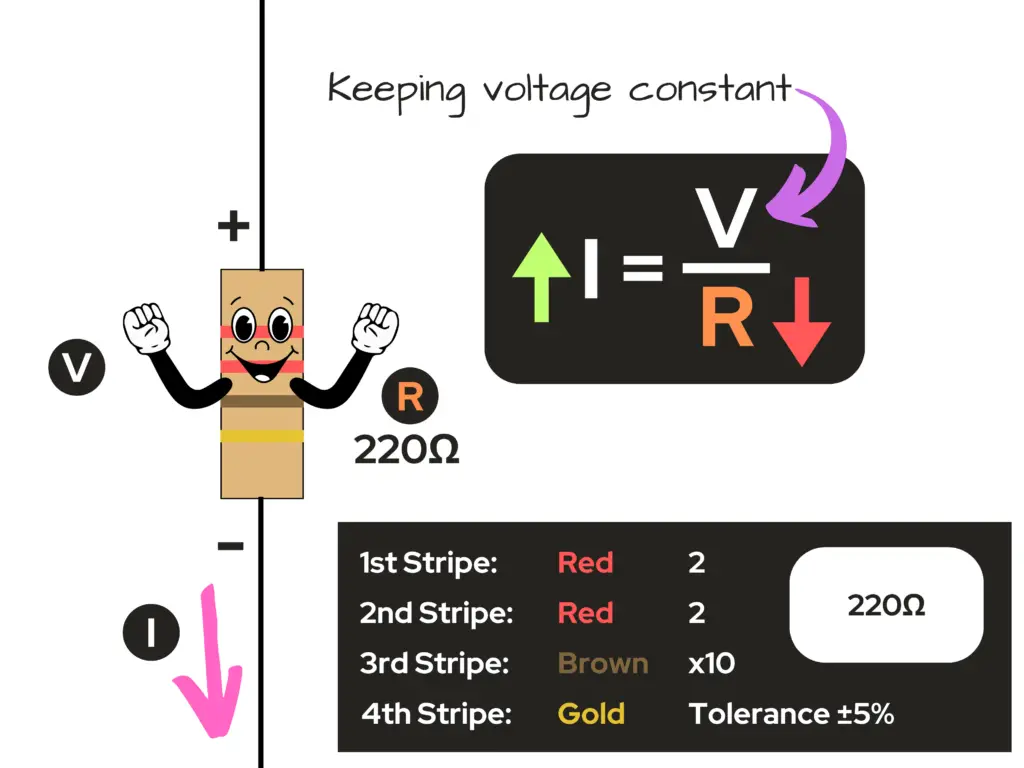
Ohm’s Law by Example
Let’s say that there’s a 220Ω resistor in a circuit with a constant source voltage of 9V. What’s the value of the circuit current?
\begin{equation}
V = IR
\end{equation}
\begin{equation}
I = \frac{V}{R}
\end{equation}
\begin{equation}
I = \frac{9V}{220\Omega}
\end{equation}
\begin{equation}
I = 0.041A
\end{equation}
\begin{equation}
\boxed{I = 41mA}
\end{equation}
A circuit with a 9V source and a 220Ω resistor in series in the circuit gives a current of 41mA, flowing through the conductor and resistor in the circuit.
Keeping Voltage Constant – Higher Resistance, Less Current Flow
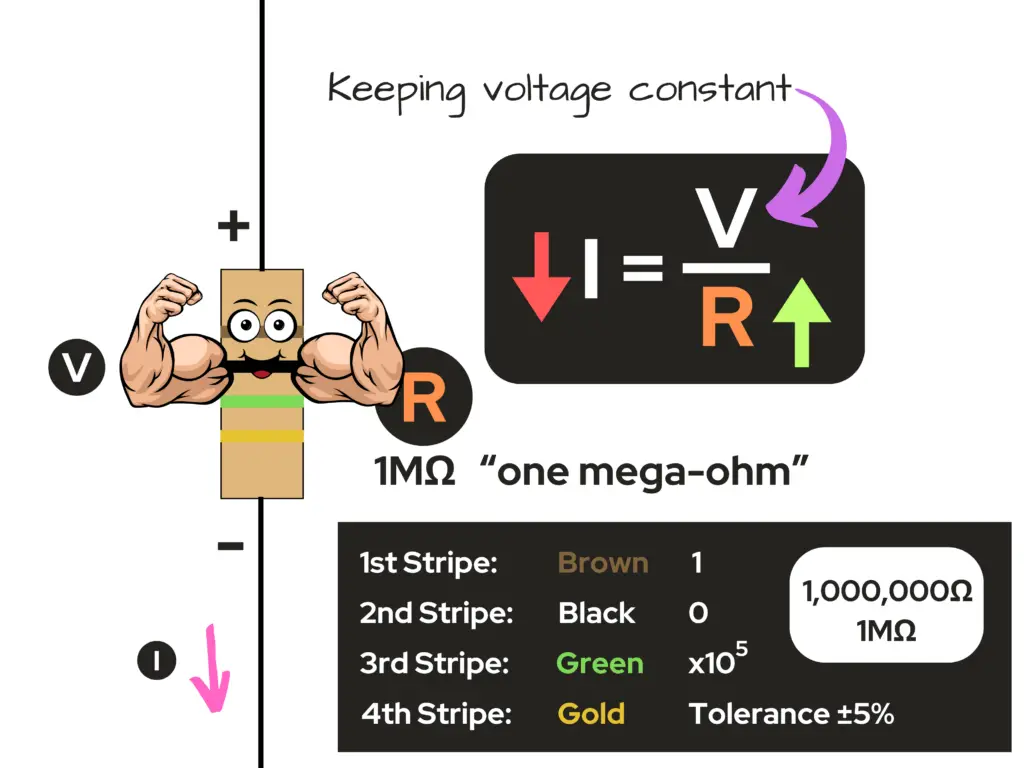
Ohm’s Law by Example
Let’s say that we replace the 220Ω resistor in our circuit from before, with a 1MΩ resistor in the circuit with a constant source voltage value of 9V. What’s the value of the circuit current now?
\begin{equation}
V = IR
\end{equation}
\begin{equation}
I = \frac{V}{R}
\end{equation}
\begin{equation}
I = \frac{9V}{1M\Omega}
\end{equation}
\begin{equation}
I = \frac{9V}{1,000,000\Omega}
\end{equation}
\begin{equation}
I = 0.000009A
\end{equation}
\begin{equation}
\boxed{I = 9\mu A}
\end{equation}
A circuit with a 9V source and a 1MΩ resistor in series in the circuit gives a current of 9µA flowing through the conductor and resistor in the circuit. That’s a 99.978 percent decrease from the value of current with the 220Ω resistor!
Conclusion
You’ve learned that Ohm’s Law helps us describe important characteristics within a circuit, such as voltage, current and resistance. You learned that Ohm’s law states that a voltage applied to a circuit is proportional to the product of the current flowing through the circuit and the circuit’s resistance.
Knowing what you know now about Ohm’s Law, if given a circuit with a voltage applied across a known resistance value in the circuit, you could find the current through that resistance — or, if given the current and resistance in the circuit, you could find the voltage applied across the resistance — or, if given the voltage and current of the circuit, you could find the value of resistance.
Having the knowledge and understanding of Ohm’s Law is the gateway into the world of electronics and electrical engineering. It’s a stepping stone in learning more about how circuits work and other laws you’ll learn if furthering your electrical education, such as Kirchhoff’s Voltage Law and Kirchhoff’s Current Law. You’re really on your way to becoming a bona fide electronics or robotics engineer! Just remember to keep at it and stay motivated!


