Ohm’s Law is one of the most fundamental principles in electricity and electronics, and it’s what helps us to describe the relationship of the current through a conductor between two points in a circuit and its direct proportionality to the electric potential difference, or voltage across those two points.

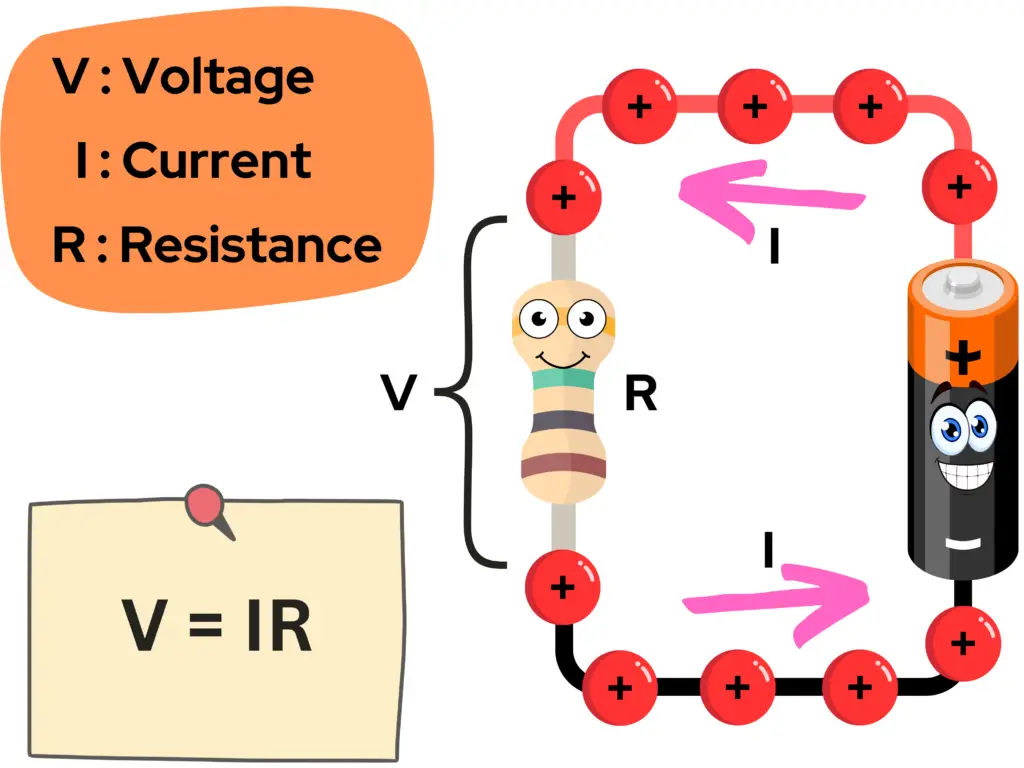
Ohm’s law is the relationship between three units of measure in electronics – voltage, current and resistance. It states that the product of the current flowing through a conductor in a circuit and a resistance along the conductor in the circuit is directly proportional to the voltage applied across the resistance.

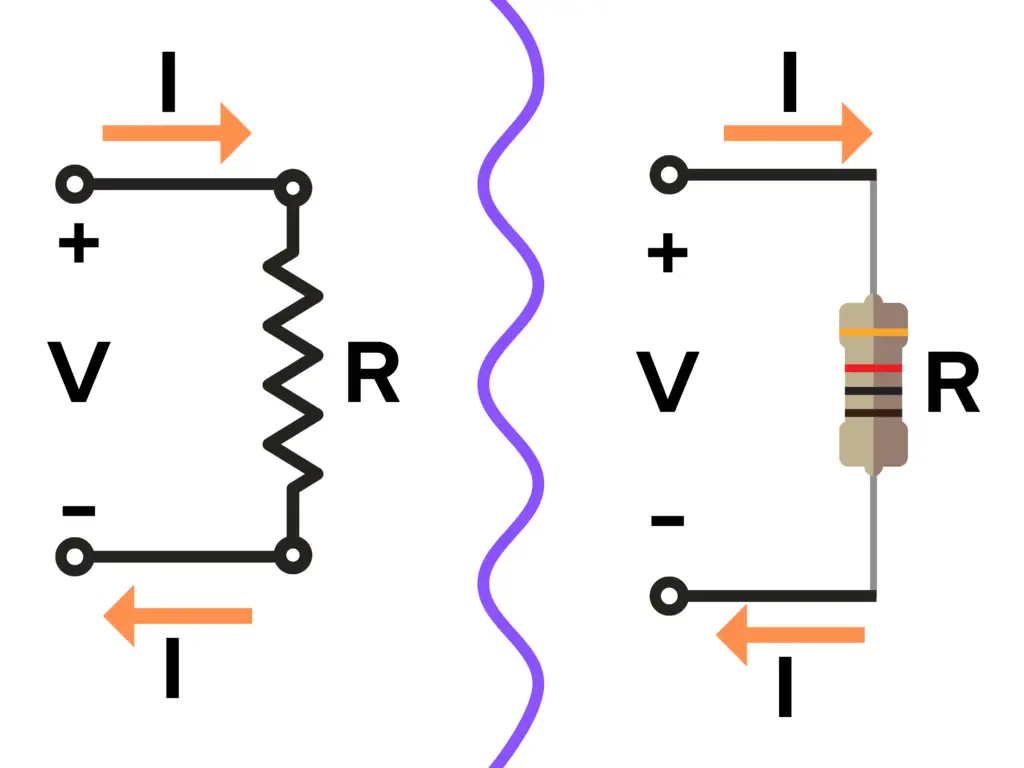
Said another way, Ohm’s Law states that for a given resistance and an electric current flowing through that resistance, there is an electric voltage potential across that resistance.

Ohm’s Law

The formula for Ohm’s Law shows that for a given resistance, the product of the resistance (R) and the current (I) are proportional to (equal to) the voltage (V) across that resistance:

\begin{equation}\label{eq:NL}
V = IR
\end{equation}

In words: “Voltage equals Current multiplied by the Resistance“

---

Ohm’s Law: The Water and Car Cleaning Analogy

Let’s say that it’s a beautiful summer day and your car is filthy. You think to yourself, “today is the perfect day to wash my car!” So, you grab your cleaning supplies and bucket of suds to start cleaning off the dust, dirt, mud, and bugs off your vehicle.

We’ll use the imagery of washing your car and our imagination to do an analogous comparison of electrical properties and car washing to help us understand Ohm’s Law a bit better.

---

Voltage

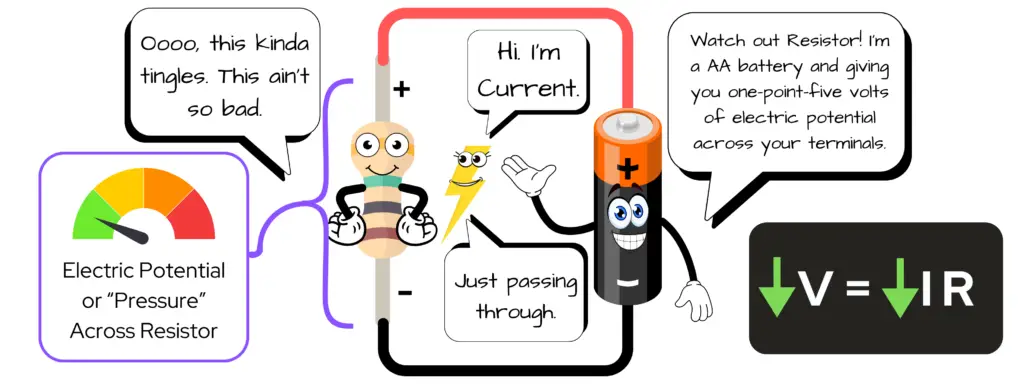
The voltage or electric potential difference measures the force that pushes electric charges through a conductor – the unit of measure being “volts”, represented by a V. Voltage is typically supplied by a power source, such as a battery or from a wall outlet.

Low Water Pressure

Using our water and car cleaning analogy, you can think of voltage as being the amount of water pressure your water hose has and the voltage source, such as a battery, as being the source of water that comes from your local city’s water supply.

The lower the water pressure, such as a trickle out of your hose – the less pressure and power you’ll have to force the water through the nozzle to be able to spray the mud off your tires and fenders – the more time you’re going to spend scrubbing.

Low Voltage

The lower the voltage, the less current flow and less power a circuit has – as long as the resistance stays constant.

Ohm’s Law by Example Say you’re given the current and resistance of a circuit. The current through the circuit and resistor is 30 milliamps and the resistor value is 50 ohms. Find the voltage across the resistance.
\begin{equation}
V = IR
\end{equation}

\begin{equation}
V = (30mA)(50\Omega)
\end{equation}

\begin{equation}
V = (0.030A)(50\Omega)
\end{equation}

\begin{equation}
\boxed{V = 1.5V}
\end{equation}

High Water Pressure

The higher the water pressure, such as with using a pressure washer – the more pressure and power you’ll have to force the water through the nozzle to be able to blast the mud right off your car within seconds.

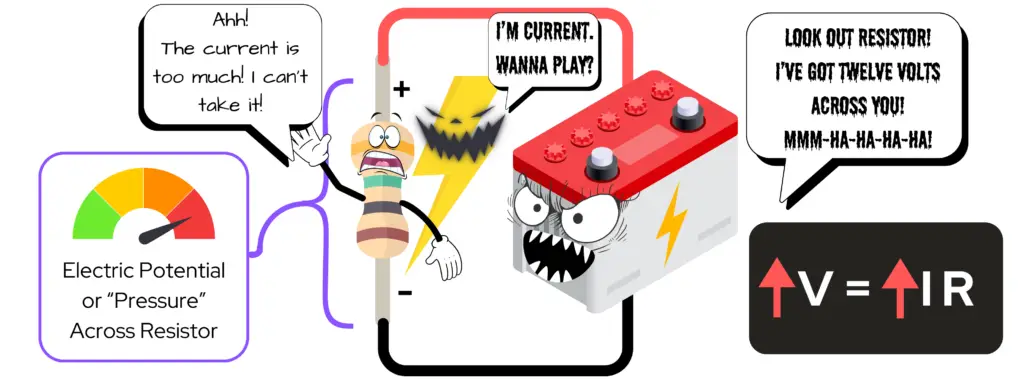
High Voltage

The higher the voltage, the more current flow and more power a circuit has – as long as the resistance stays constant.

Ohm’s Law by Example Say you’re given the current and resistance of a circuit. The current through the circuit and resistor is 240 milliamps and the resistor value is 50 ohms. Find the voltage across the resistance.
\begin{equation}
V = IR
\end{equation}

\begin{equation}
V = (240mA)(50\Omega)
\end{equation}

\begin{equation}
V = (0.240A)(50\Omega)
\end{equation}

\begin{equation}
\boxed{V = 12V}
\end{equation}

---

Current

Current refers to the rate at which electric charges flow through a conductor during a given amount of time – the unit of the measure of current is the Ampere or “amp”, represented by an A. An amp is defined as one coulomb of charge moving past an area of a conductor in one second.

• 1 coulomb of charge is equal to the electric charge delivered by 1 ampere of current in 1 second.
• 1 coulomb is defined in terms of the elementary charge e.
• e ≈ 6.241509 x 10¹⁸ electrons

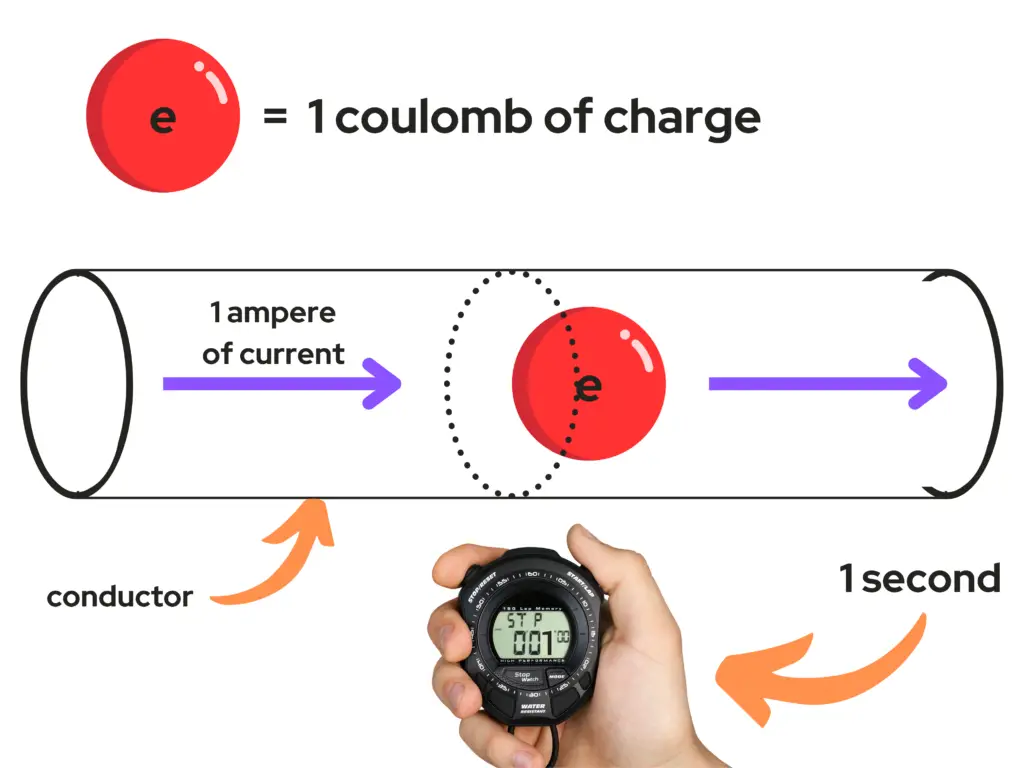
As you can see from the image above, I’ve represented a red ball as 1 coulomb of charge. I’ve used a red ball because making an image with 6,241,509,000,000,000,000 electrons would have taken me about 200,000,000,000 years at a rate of adding an electron to the image every second! Not ideal.

Our 1 coulomb red ball is being delivered through the conductor by 1 ampere of current and passes through the area of the conductor represented by the dotted section. When 6.241509×10¹⁸ electrons passes through that area of the conductor in 1 second, then we have 1 coulomb of charge – represented by the red ball.

Lower Water Pressure, Less Water Flow – Higher Water Pressure, More Water Flow

Using our water and car cleaning analogy, we can think of current as being how much water is coming out the end of the water hose at a given rate of time.

The lower the water flow, such as a trickle out of your hose – the less water flowing out the end of the water hose at a given moment in time – the less water force you have from your water hose to wash your car.

The higher the water flow, such as when you turn the water fully on at the valve – the more water flowing out the end of the water hose at a given moment in time – the more water force you have from your water hose to wash your car.

Lower Voltage, Less Current Flow

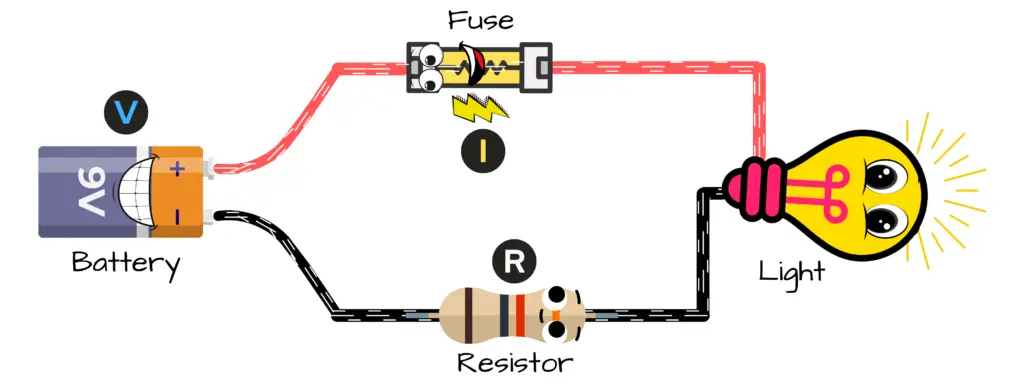
Ohm’s Law by Example Say you’re given the voltage and resistance of a circuit. The voltage across the resistance in the circuit is 9 volts and the resistor value is 1000 ohms. Find the value of current through the resistance.
\begin{equation}
V = IR
\end{equation}

\begin{equation}
I = \frac{V}{R}
\end{equation}

\begin{equation}
I = \frac{9V}{1000\Omega}
\end{equation}

\begin{equation}
I = 0.009A
\end{equation}

\begin{equation}
\boxed{I = 9mA}
\end{equation}

Higher Voltage, More Current Flow

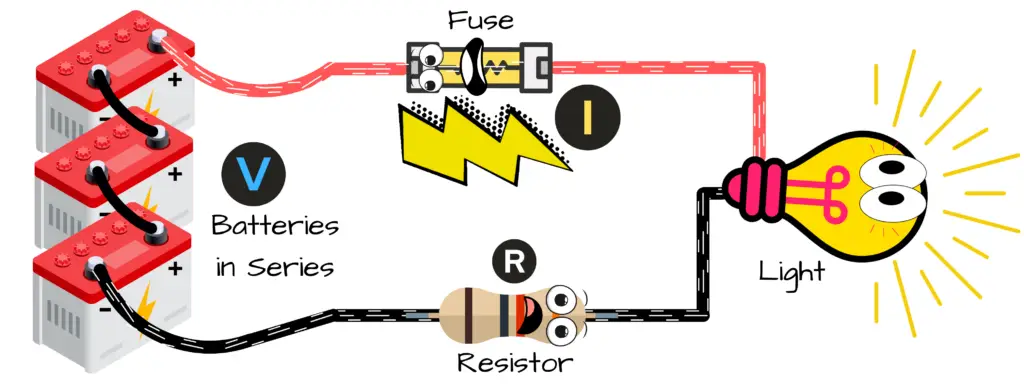
Ohm’s Law by Example Say you’re given the voltage and resistance of a circuit. The voltage across the resistance in the circuit is 36 volts and the resistor value is 1000 ohms. Find the value of current through the resistance.
\begin{equation}
V = IR
\end{equation}

\begin{equation}
I = \frac{V}{R}
\end{equation}

\begin{equation}
I = \frac{36V}{1000\Omega}
\end{equation}

\begin{equation}
I = 0.036A
\end{equation}

\begin{equation}
\boxed{I = 36 mA}
\end{equation}

---

Resistance

Resistance refers to the property of material that opposes the flow of electric current. Said another way — it is the ability of a material to resist the flow of current. A resistance in a circuit is given the unit of measure in “ohms”, using the capital Greek letter Ω, called “Omega”.

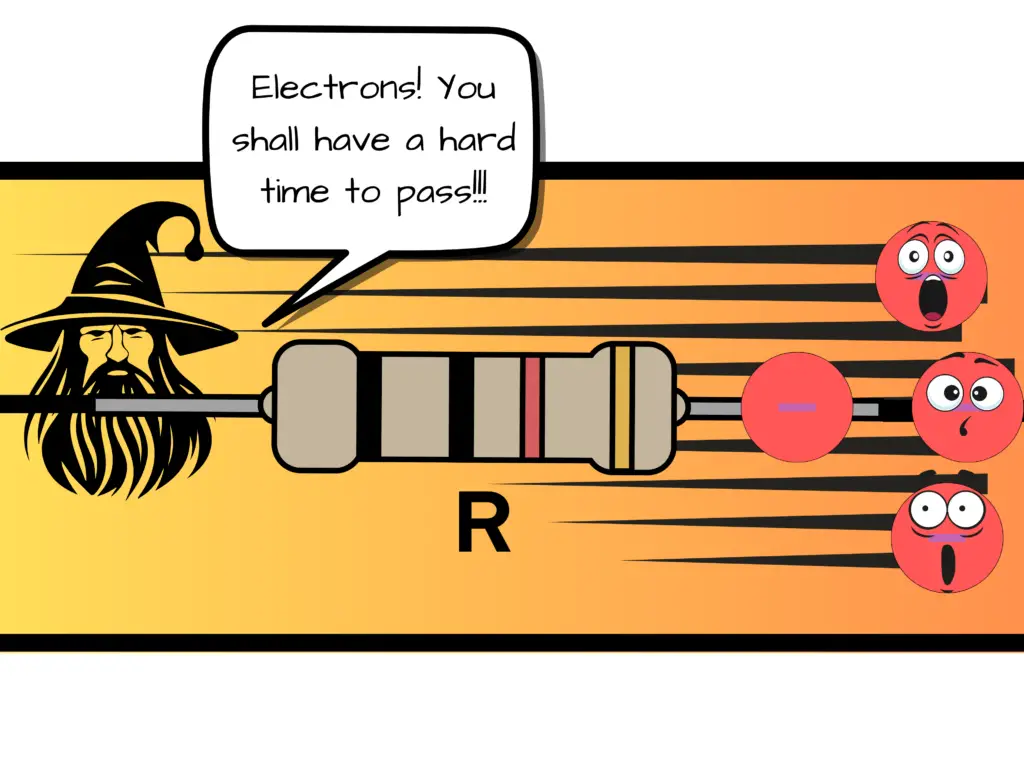
Using our water and car cleaning analogy, we can think of a resistance as being a kink in our water hose – You know when you’re using the water hose and it folds on itself not allowing water to flow through it like it should? – That’s a kink, or a resistance to the flow of water.

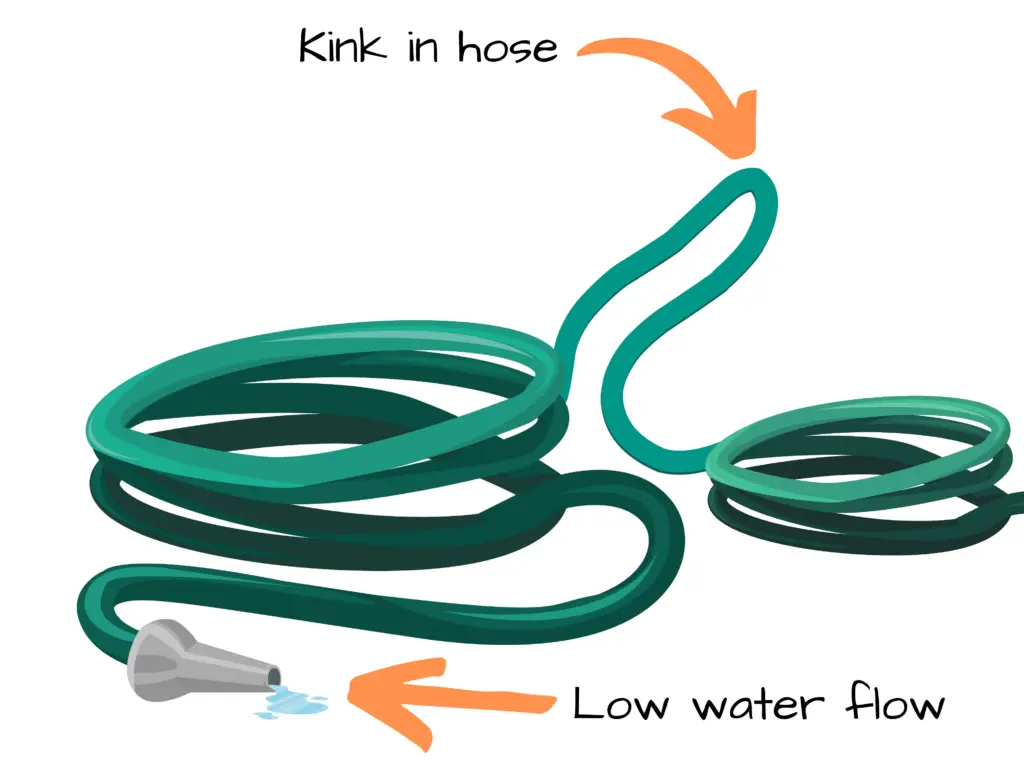
When we take the kink out of the hose – so there’s no obstruction or resistance of flow for the water – then our water hose can provide a stream of water again.

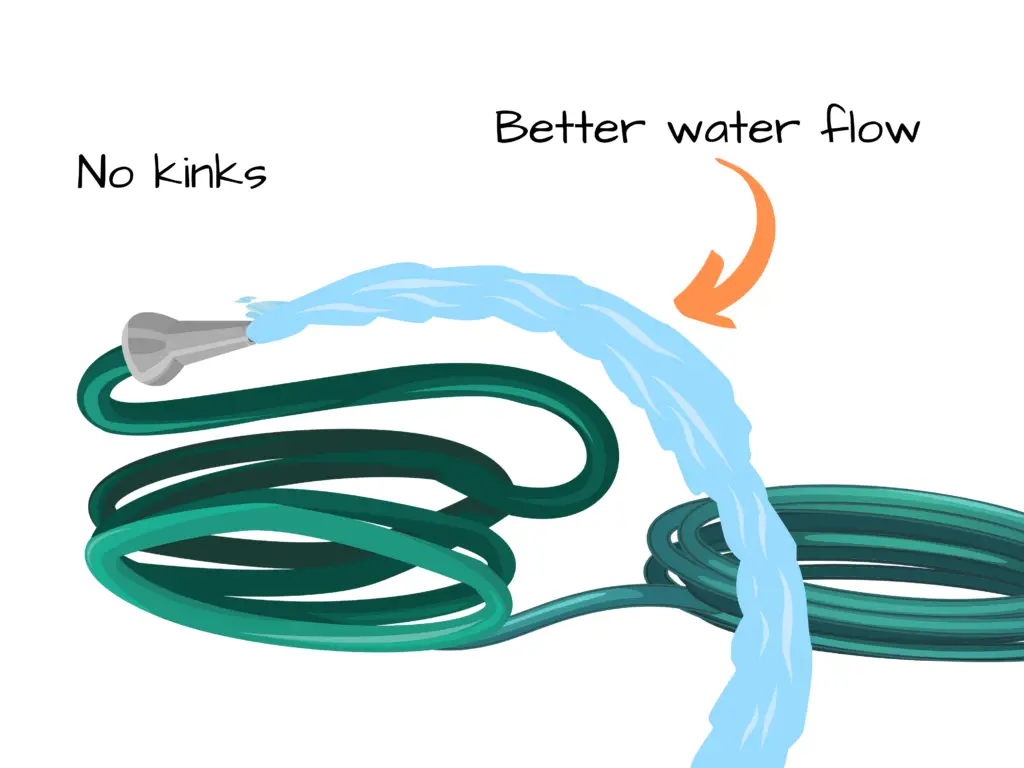
Keeping Voltage Constant – Lower Resistance, More Current Flow

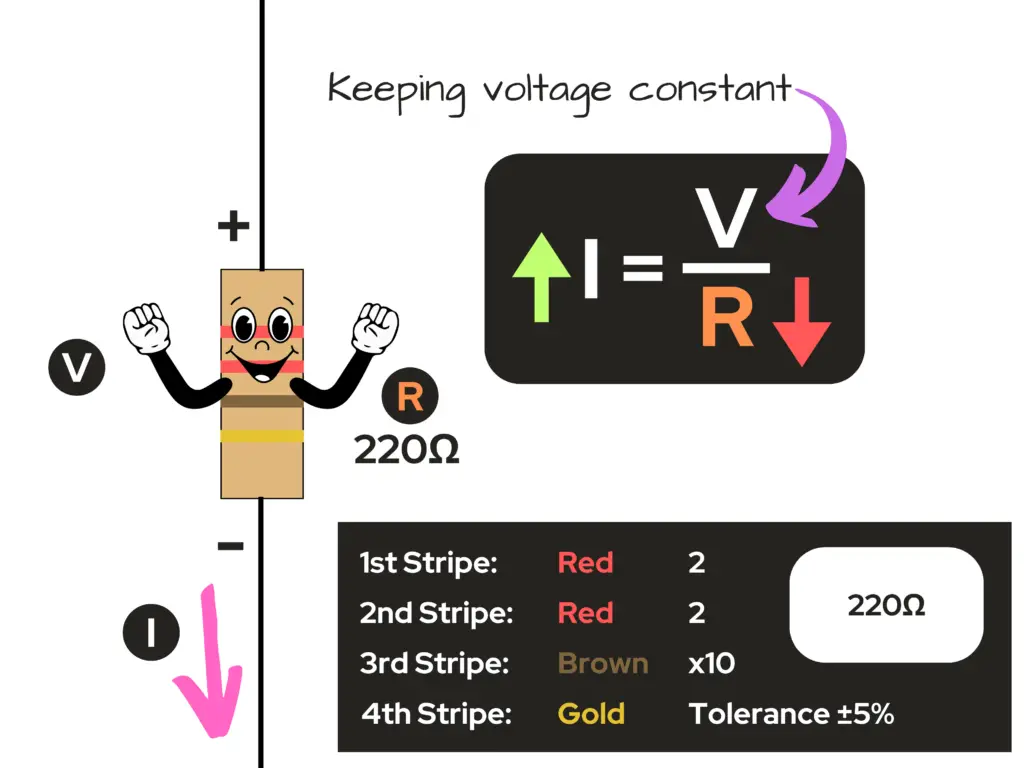
Ohm’s Law by Example Let’s say that there’s a 220 ohm resistor in a circuit with a constant voltage value of 9 volts across the resistor. What’s the value of the current flowing through the resistor in the circuit?
\begin{equation}
V = IR
\end{equation}

\begin{equation}
I = \frac{V}{R}
\end{equation}

\begin{equation}
I = \frac{9V}{220\Omega}
\end{equation}

\begin{equation}
I = 0.041A
\end{equation}

\begin{equation}
\boxed{I = 41mA}
\end{equation}

A circuit with a 9 volt source and a 220 ohm resistor in series in the circuit gives a current of 41 mill-amps flowing through the conductor and resistor in the circuit.

Keeping Voltage Constant – Higher Resistance, Less Current Flow

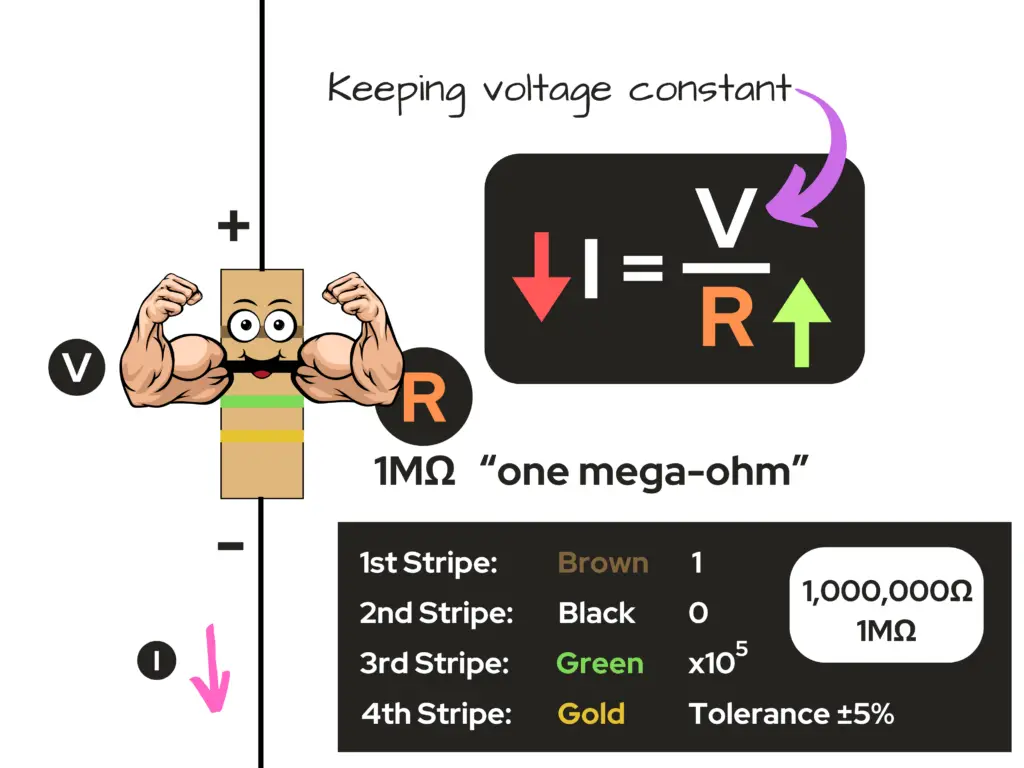
Ohm’s Law by Example Let’s say that we replace the 220 ohm resistor with a 1 mega-ohm resistor in the circuit with a constant voltage value of 9 volts across the resistor. What’s the value of the current flowing through the resistor in the circuit now?
\begin{equation}
V = IR
\end{equation}

\begin{equation}
I = \frac{V}{R}
\end{equation}

\begin{equation}
I = \frac{9V}{1M\Omega}
\end{equation}

\begin{equation}
I = \frac{9V}{1,000,000\Omega}
\end{equation}

\begin{equation}
I = 0.000009A
\end{equation}

\begin{equation}
\boxed{I = 9\mu A}
\end{equation}

A circuit with a 9 volt source and a 1 mega-ohm resistor in series in the circuit gives a current of 9 micro-amps flowing through the conductor and resistor in the circuit. That’s a 99.978% decrease from the value of current with the 220Ω resistor!

---

Conclusion

You’ve learned that Ohm’s Law helps us describe important characteristics within a circuit, such as voltage, current and resistance. You learned that Ohm’s law states that a current flowing through a conductor and resistance in a circuit is proportional to the voltage applied across the resistance in the circuit.

Knowing what you know now about Ohm’s Law, if given a circuit with a voltage applied across a known resistance in the circuit, you could find the current through that resistance — or, if given the current and resistance in the circuit, you could find the voltage applied across the resistance — or, if given the voltage and current of the circuit, you could find the resistance.

Having the knowledge and understanding of Ohm’s Law is the gateway into the world of electronics and electrical engineering. It’s a stepping stone in learning more about how circuits work and other laws you’ll learn if furthering your electrical education, such as Kirchhoff’s Voltage and Current Laws. You’re really on your way to becoming a bona fide electronics or robotics engineer, or even an electrician! Just remember to keep at it and stay motivated!