An ideal current source is a source of constant current to a system, independent of the source voltage. An ideal current source provides this constant current with 100% efficiency — it has an internal parallel resistance with a value that is infinite.

A practical current source is a device that supplies current to a system, yet unlike an ideal current source, has some internal resistance in parallel within itself. It cannot fully provide all of its current capabilities due to having some internal resistance, therefore it is not 100% efficient.

What’s a Source?

A source is any device that delivers energy into to a system — whereas, a device that extracts or consumes energy from a system is known as an electrical load.

Sources convert mechanical, chemical, thermal and other forms of energy into electrical energy — such as a 9V battery converting chemical energy into electrical energy. A source is considered to be an active element that generates electrical energy in some way.

Two Kinds of Sources

1. Voltage Source: A device capable of supplying a voltage to a circuit. A voltage source supplies energy or power to a circuit in the form of a voltage potential.
2. Current Source: A device capable of supplying a current to a circuit. A current source supplies energy or power to a circuit in the form of current.

A Review of Power in a Circuit

Recall the definition of power in purely resistive circuits is the measure of how much work or energy transfer the circuit can do over an amount of time. The formula for power is given as the product of the voltage (V) across a purely resistive element and the current (I) through that element — or what I like to call “piv”:

\begin{equation}
P = IV
\end{equation}

Recall Ohm’s Law (V = IR). Power (P) can also be written as:

\begin{equation}
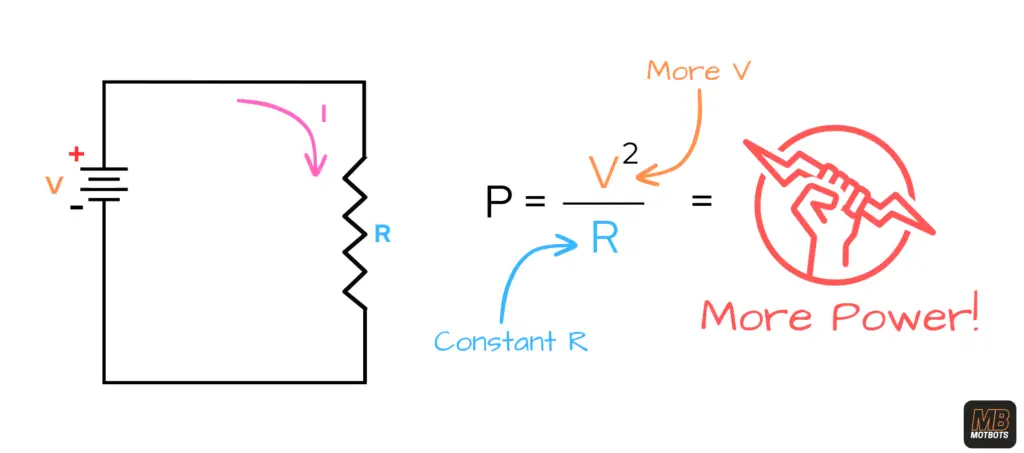
P\space =\space \frac{V^2}{R}
\end{equation}

or written as:

\begin{equation}
P\space =\space {I^2}R
\end{equation}

Looking at the power formula above, we see that for a circuit with constant resistance (R), an increase in current (I) to a circuit will increase its power (P) — on the other hand, if there’s a decrease in current (I) to a circuit, then there is a decrease in it’s power (P).

Preliminary Concepts You May Want to Review

Before continuing on with our discussion of ideal current sources, you may want to consider looking further into the circuit theory of active and passive components here. Having a good understanding of active and passive components — and what they are — will greatly increase your understanding of current sources.

You may also want to consider looking at our page entitled Circuit Theory: Circuit Nodes, Loops and Meshes here, since we’ll be discussing concepts that are tangential to current loops within a circuit later in our discussion.

Ideal Current Source

It was briefly mentioned earlier that an active element is the circuit component that supplies energy to other circuit components — it delivers power or energy to a circuit. Again, I suggest you read up on active and passive elements here, if you’re not familiar with these concepts.

An ideal current source is a device capable of supplying a constant current to a circuit with respect to time, and is free from the influence of voltage from the circuit. In short, an ideal current source delivers a prescribed current independent of the voltage supplied to the circuit it is associated with.

Characteristics of an Ideal Current Source

• An ideal current source refers to a source that consistently maintains a constant supply of current to a circuit, regardless of the resistance of the load or voltage supplied to the circuit.
• What this means is that no matter the resistance in a circuit’s load —or thevoltage potential across it, the ideal current source will always provide a constant current.
• An ideal current source acts to provide 100% efficiency of current supply — meaning that the source has infinite internal resistance.
• The internal resistance of an ideal current source is infinite and in parallel with the source.

What Does It Mean to Have Infinite Internal Resistance?

As stated earlier, an ideal current source acts to provide 100% efficiency of current supply to a circuit — it has infinite internal resistance. Let’s take a look at the following circuit with a labeled internal resistance (R_in) of a current source:

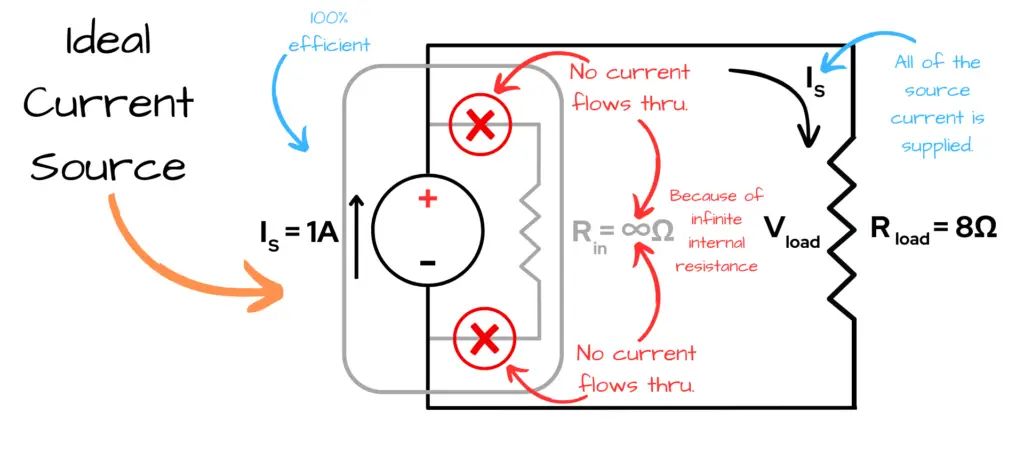
In order to provide this so-called 100% efficiency, there has to be an infinite internal resistance in the source to provide the entire source current (I_S = 1A) through the resistive load of 8Ω in the circuit — hence, an ideal current source.

Again, having infinite internal resisance (R_in = ∞Ω) in the current source means that the source, in theory, could provide all of its current to the load. This is not possible!

Why is not possible for a current source to deliver all of its current to a system?

Just like for a voltage source, in all practicality, there’s always some internal resistance — not zero, for the case of ideal voltage sources — not infinite, for the case of ideal current sources, but some internal resistance. This internal resistance comes from the nature of the structural makeup of the source device itself.

Looking Further Into the Details

Let’s look at the image of the ideal current source again:

Let’s review what our ideal current source circuit is telling us from the image above:

• Our ideal current source has an infinite internal resistance (R_in = ∞Ω) and a given source current (I_S) value of 1A.
• The gray box around our source current (I_S) and internal resistance (R_in) represents the ideal current source device as a whole.
• The internal resistance is grayed-out because we’re considering this device in our circuit as our ideal current source — meaning it has an infinite internal resistance, therefore there is no source current (I_S) flowing through this part of the system — current is taking the path of least resistance.
• Since this is an ideal current source, all of the source current is supplied to the load — meaning the full 1A of source current flows through the load and returns back to the source, completing the loop in the circuit.

If our source is ideal, that means that the current through the load must be always constant and equal to the current source, I_S — this must be true no matter the value of the load resistance (R_load).

The statement “this must be true no matter the value of the load resistance (R_load)” is telling us that the internal resistance (R_in) of the current source must be infinite — i.e. ideal.

17. Why?

1. Recall the concept of current flow and open circuits — according to our circuit above, to have the current not flow through the branch of the circuit where the internal resistance is, then the internal resistance must be infinite — i.e. an ideal current source. In other words, the internal resistance is like an open circuit in that branch of the circuit because of its infinite resistance. This means that there is only one way for the current from the source to flow, and that’s for all of it to flow through the load.

Let’s understand this concept with the following representation of a current source and its internal resistance in a circuit with a load:

Notice node A in the circuit. Recall that current entering a node in a circuit must equal to the current leaving the node.

If we were to take a magical magnifying glass that allows us to see current and look closer at node A, we’d see the source current entering the node and both the branch of internal current and branch of load current leaving the node:

So, the current through the load would be:

\begin{equation}
I_{load}\space = \space I_S\space -\space I_n
\end{equation}

Recalling Ohm’s Law and rearranging, we get:

\begin{equation}
V = IR
\end{equation}

\begin{equation}
I = \frac{V}{R}
\end{equation}

We’re focusing on current that flows through the internal resistance. The internal current is:

\begin{equation}
I_n\space =\space \frac{V_S}{R_n}
\end{equation}

\begin{equation}
I_{load}\space = \space I_S\space -\space \frac{V_S}{R_n}
\end{equation}

If the current source were ideal, then the internal resistance (R_n) would be infinite:

\begin{equation}
I_{load}\space = \space I_S\space -\space \frac{V_S}{∞}
\end{equation}

and division by ∞ is zero — because the larger the denominator gets in the rational, the smaller the value of the rational gets. In this case, the value gets super close to zero when R_n becomes infinite, so we say the rational tends to the value of zero:

\begin{equation}
I_{load}\space = \space I_S\space -\space 0
\end{equation}

\begin{equation}
I_{load}\space = \space I_S
\end{equation}

So, for an ideal current source the current through the load is equal to the source current.

Practical Current Source

In reality, there’s always some sort of internal resistance in a current source that’s nearer in value to the load resistance — much closer to its value than being infinite.

An internal resistance is present, but no where near being infinite. These losses due to the internal resistance comes from the physical makeup of the source itself — this is what’s called a practical current source.

A practical current source is a device that supplies current to a circuit, yet unlike an ideal current source, it hasaninternal resistance closer in value than being infinite to the load resistance and is in parallel withthe source. This parallel resistance causes a division in current when current passes through the source causing slight variations in the amount of source current reaching a load.

Practical Current Source Example:

Let’s say you have a current source. Your current source is a Theoretical Black-Box from Theory, Inc., that seems to state that it can supply an ideal source current of 1A. It’s label says “1 amp for $3.99 —It’s ideal for this deal!”

“Hmm. Seems to be some marketing going on here”, your buddy thinks to himself.

You connect the Theoretical Black-Box to your circuit and take a multimeter to measure the amount of current through your 8Ω load, to make sure it’s receiving the ideal 1A of current. You measure the current to find out that your meter reads 714mA, not 1A. You say to yourself, “Hey, this thing is busted! What a gyp! Now I’ve got to return it to get my money back!”

Your buddy, seeing your ignorance in current sources, stops you and tells you that the device has some internal resistance, and therefore cannot supply the full 1A to your load. He tells you, “It’s the marketers, man. They got you. There’s no such thing as an ideal current source.”

He shows you the device’s datasheet, where it states that its ideal current is rated at 1A — he says, “The company is tantalizing folks to think that their device can actually do this when in reality it cannot.”

“The company’s Black-Box cannot provide this stated ideal current of 1A. The way it’s designed doesn’t allow it. They’re basically claiming it has an infinite resistance, which is impossible, man.”

Your buddy continues, “The factory shows that it has measured the actual internal resistance of its Black-Box to be 20Ω. So, in reality, your load current is going to be lesser than the product’s stated source current. In this case, you actually measured the load current to be about 714mA.”

Observing the Math of our Theoretical Black-Box Example:

Let’s observe the following calculations. We want to calculate the load current. Recall Ohm’s Law:

\begin{equation}
V = IR
\end{equation}

The source voltage across the Theoretical Black-Box is the product of the source current (I_S) and the circuit’s total resistance (R_total):

\begin{equation}
V_S\space =\space I_SR_{total}
\end{equation}

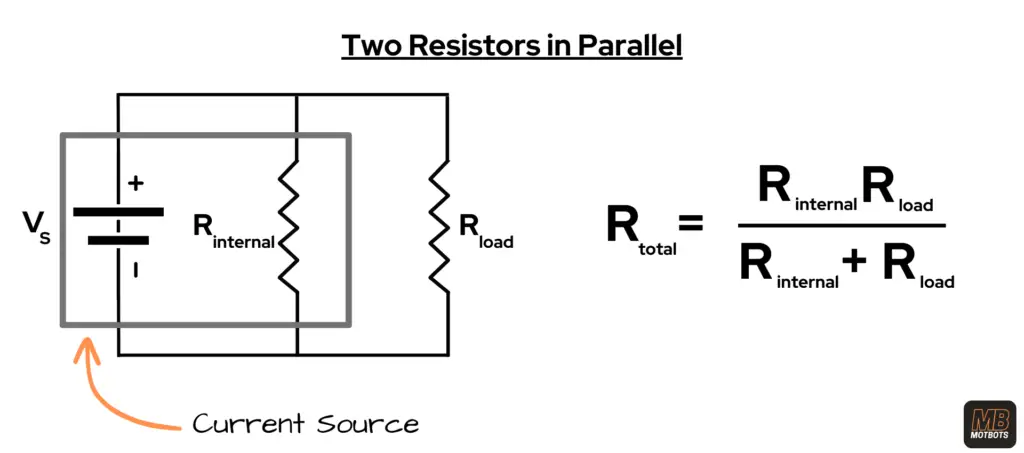
Recall, to calculate two resistors in parallel, we use the formula:

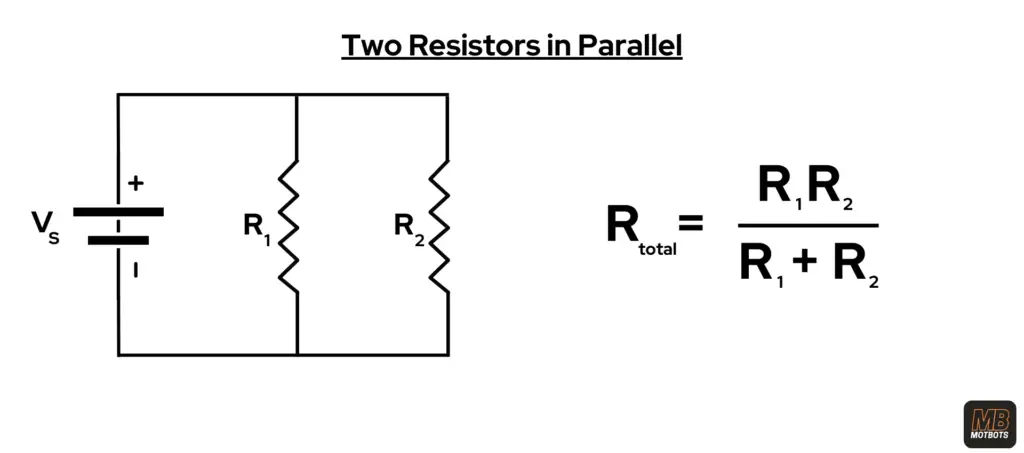
In our case, the total resistance (R_total) includes the two resistances R_internal, for the internal resistance of the source, and R_load, for the load resistance.

\begin{equation}
V_S\space =\space I_S\space \frac{R_{internal}R_{load}}{R_{internal}\space +\space R_{load}}
\end{equation}

We want to calculate our source as if it were ideal. For an ideal source, V_S = I_loadR_load, because this would mean that we’d obtain 100% efficiency — which is the situation everyone would want from this product.

\begin{equation}
I_{load}R_{load}\space =\space I_S\space \frac{R_{internal}R_{load}}{R_{internal}\space +\space R_{load}}
\end{equation}

\begin{equation}
I_{load}\space =\space I_S\space \frac{R_{internal}}{R_{internal}\space +\space R_{load}}
\end{equation}

\begin{equation}
I_{load}\space =\space 1A\space \frac{20Ω}{20Ω\space +\space 8Ω}
\end{equation}

\begin{equation}
I_{load}\space =\space 1A\space \frac{20Ω}{28Ω}
\end{equation}

\begin{equation}
\boxed{I_{load}\space =\space 0.7142857143A\space ≈\space 0.714A}
\end{equation}

Approximately 0.714A or 714mA — this is exactly what it was measured to be! This is not the ideal 100% efficiency we were looking for out of our example current source circuit.

Your Buddy Saves the Day with an Almost Ideal Current Source:

The next day, to cheer you up, your buddy brings you a surprise. It’s the True Company’s version of the Black-Box. “The True Company does people right!”, your buddy tells you.

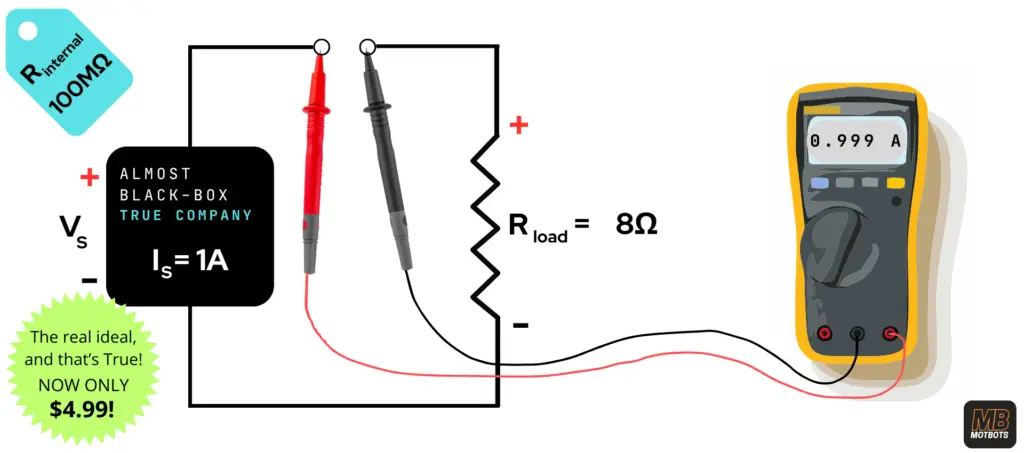
Your buddy shows you in its datasheet that the Almost Black-Box has an internal resistance of 100MΩ — “An internal resistance close enough to making the source ideal”, your buddy states.

“With this much internal resistance, this current source is almost like having a real ideal!”

You notice that its label states “Almost Black-Box True Company — The real ideal, and that’s True! NOW ONLY $4.99!”

“Hmm. It’s more than the Theoretical. Hope it lives up to the hype for that price”, you think to yourself.

You proceed to connect the Almost Black-Box to your circuit and take a multimeter to measure the amount of current through your 8Ω load. You measure the current to find out that your meter reads 999mA. You see this with surprise and say, “Hey, this thing is awesome, bud! Way better that my other Black-Box. Thanks buddy!”

Observing the Math of our Almost Black-Box Example:

Let’s observe the following calculations. We want to calculate the load current. Again, recalling Ohm’s Law:

\begin{equation}
V = IR
\end{equation}

The source voltage across the Almost Black-Box is the product of the source current (I_S) and the circuit’s total resistance (R_total):

\begin{equation}
V_S\space =\space I_SR_{total}
\end{equation}

The total resistance (R_total) includes the two resistances R_internal, for the internal resistance of the source, and R_load, for the load resistance.

\begin{equation}
V_S\space =\space I_S\space \frac{R_{internal}R_{load}}{R_{internal}\space +\space R_{load}}
\end{equation}

Again, we want to calculate our source as if it were ideal. For an ideal source, V_S = I_loadR_load, because this would mean that we’d obtain 100% efficiency — which is the situation everyone would want from this product.

\begin{equation}
I_{load}R_{load}\space =\space I_S\space \frac{R_{internal}R_{load}}{R_{internal}\space +\space R_{load}}
\end{equation}

\begin{equation}
I_{load}\space =\space I_S\space \frac{R_{internal}}{R_{internal}\space +\space R_{load}}
\end{equation}

\begin{equation}
I_{load}\space =\space 1A\space \frac{100\space MΩ}{100\space MΩ\space +\space 8Ω}
\end{equation}

\begin{equation}
I_{load}\space =\space 1A\space \frac{100,000,000Ω}{100,000,008Ω}
\end{equation}

\begin{equation}
I_{load}\space =\space 0.99999992A\space ≈\space 1A
\end{equation}

The outcome is very close to 1A and almost ideal!

Conclusion

We stared off going over sources and what they are. You learned that a source is any device that delivers energy into a system. We further expanded the idea of sources into their ideal and practical situations.

You learned that an ideal current source is a type of source that provides all of its current through its terminals — that it is a source with an infinite internal resistance. You learned that a practical current source is the real world version of a source, which does consider its internal resistance and that the current through the load is determined by how close in value the source’s internal resistance is to the load resistance.

Our discussion continues on ideal and practical voltage sources of which you can learn about on our page entitled Circuit Theory: Ideal and Practical Voltage Sources here. Remember, keep at it and stay motivated!